Problem of The Day: Pow(x, n)

Problem Statement

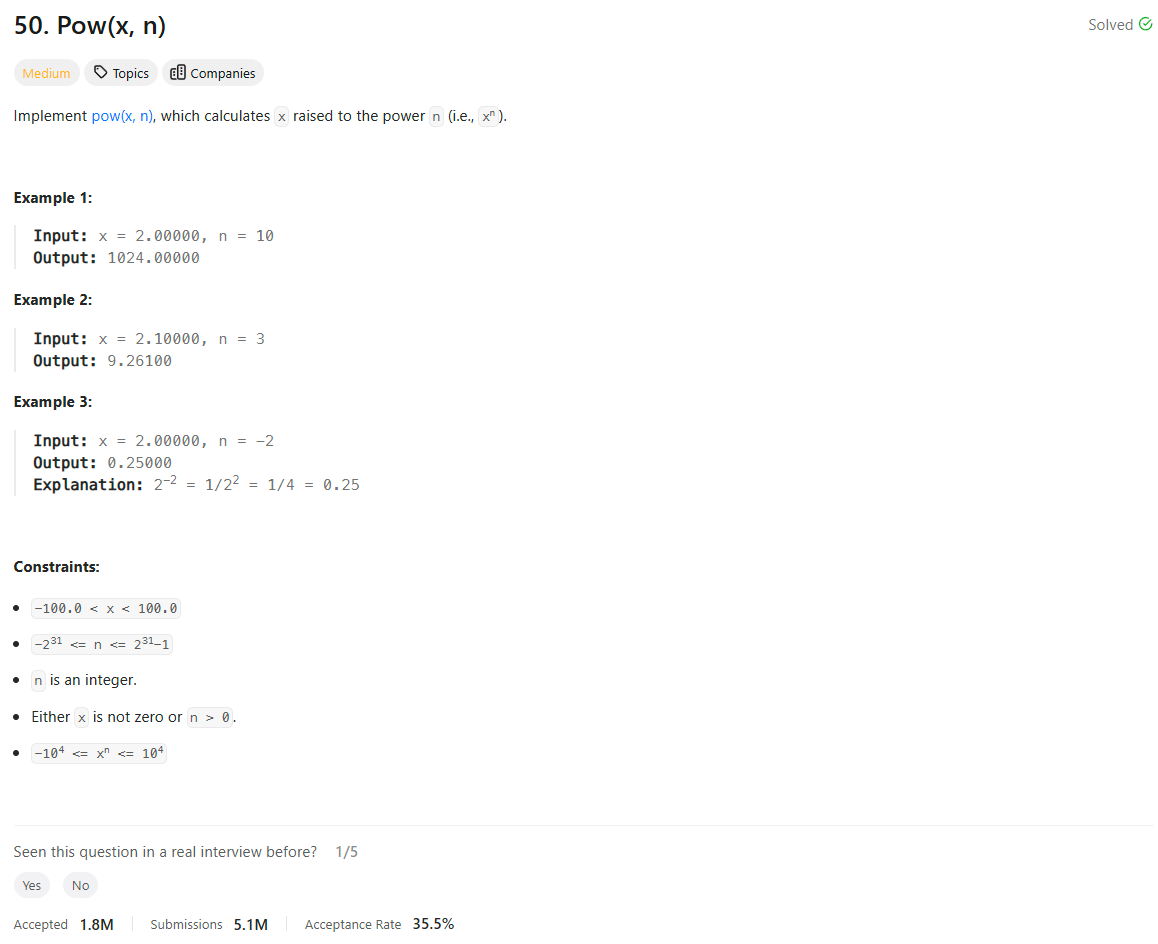
Editorial

Optimized Recursion Approach

Notes from solution:

class Solution:
    def binaryExp(self, x: float, n: int) -> float:
        # Base case, to stop recursive calls.
        if n == 0:
            return 1

        # Handle case where, n < 0.
        if n < 0:
            return 1.0 / self.binaryExp(x, -1 * n)

        # Perform Binary Exponentiation.
        # If 'n' is odd we perform Binary Exponentiation on 'n - 1' and multiply result with 'x'.
        if n % 2 == 1:
            return x * self.binaryExp(x * x, (n - 1) // 2)
        # Otherwise we calculate result by performing Binary Exponentiation on 'n'.
        else:
            return self.binaryExp(x * x, n // 2)

    def myPow(self, x: float, n: int) -> float:
        return self.binaryExp(x, n)

• time: O(log n)
• space: O(log n)

Approach 2: Binary Exponentiation (Iterative)

class Solution:
    def binaryExp(self, x: float, n: int) -> float:
        if n == 0:
            return 1

        # Handle case where, n < 0.
        if n < 0:
            n = -1 * n
            x = 1.0 / x

        # Perform Binary Exponentiation.
        result = 1
        while n != 0:
            # If 'n' is odd we multiply result with 'x' and reduce 'n' by '1'.
            if n % 2 == 1:
                result *= x
                n -= 1
            # We square 'x' and reduce 'n' by half, x^n => (x^2)^(n/2).
            x *= x
            n //= 2
        return result

    def myPow(self, x: float, n: int) -> float:
        return self.binaryExp(x, n)

• time: O(log n)
• space: O(1)