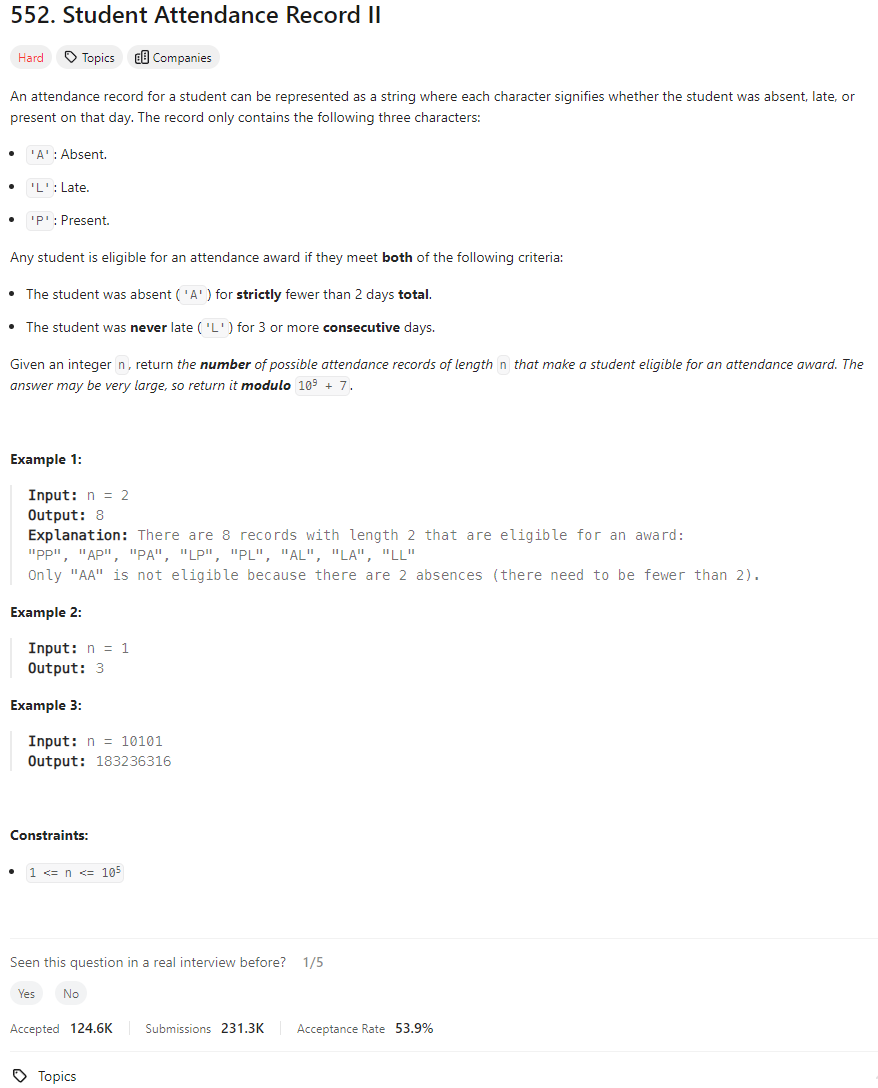
Problem Statement
Backtrack (Brute force) Approach - TLE
class Solution:
def checkRecord(self, n: int) -> int:
status = ['A', 'L', 'P']
MOD_CONST = 10**9 + 7
self.not_eligible_records = 0
def check(curr):
counter = Counter(curr)
if counter['A'] >= 2:
return True
for i in range(len(curr)):
count = 0
j = i
while j < len(curr) and curr[j] == 'L':
count += 1
j += 1
if count == 3:
return True
return False
def dfs(curr):
if len(curr) == n:
if check(curr):
self.not_eligible_records += 1
return
for j in range(3):
dfs(curr + [status[j]])
dfs([])
return 3 ** (n % MOD_CONST) - self.not_eligible_records
Editorial
Approach 1: Top-Down Dynamic Programming with Memoization
class Solution:
def checkRecord(self, n: int) -> int:
MOD = 1000000007
# Initialize the cache to store sub-problem results.
memo = [[[-1] * 3 for _ in range(2)] for _ in range(n + 1)]
# Recursive function to return the count of combinations
# of length 'n' eligible for the award.
def eligible_combinations(n, total_absences, consecutive_lates):
# If the combination has become not eligible for the award,
# then we will not count any combinations that can be made using it.
if total_absences >= 2 or consecutive_lates >= 3:
return 0
# If we have generated a combination of length 'n' we will count it.
if n == 0:
return 1
# If we have already seen this sub-problem earlier,
# we return the stored result.
if memo[n][total_absences][consecutive_lates] != -1:
return memo[n][total_absences][consecutive_lates]
# We choose 'P' for the current position.
count = eligible_combinations(n - 1, total_absences, 0)
# We choose 'A' for the current position.
count = (
count +
eligible_combinations(n - 1, total_absences + 1, 0)
) % MOD
# We choose 'L' for the current position.
count = (
count +
eligible_combinations(n - 1,
total_absences,
consecutive_lates + 1)
) % MOD
# Return and store the current sub-problem result in the cache.
memo[n][total_absences][consecutive_lates] = count
return count
# Return count of combinations of length 'n' eligible for the award.
return eligible_combinations(n, 0, 0)
Approach 2: Bottom-Up Dynamic Programming
class Solution:
def checkRecord(self, n: int) -> int:
MOD = 1000000007
# Cache to store sub-problem results.
dp = [[[0] * 3 for _ in range(2)] for _ in range(n + 1)]
# Base case: there is 1 string of length 0 with zero 'A' and zero 'L'.
dp[0][0][0] = 1
# Iterate on smaller sub-problems and use the current smaller sub-problem
# to generate results for bigger sub-problems.
for length in range(n):
for total_absences in range(2):
for consecutive_lates in range(3):
# Store the count when 'P' is chosen.
dp[length + 1][total_absences][0] = (
dp[length + 1][total_absences][0] +
dp[length][total_absences][consecutive_lates]
) % MOD
# Store the count when 'A' is chosen.
if total_absences < 1:
dp[length + 1][total_absences + 1][0] = (
dp[length + 1][total_absences + 1][0] +
dp[length][total_absences][consecutive_lates]
) % MOD
# Store the count when 'L' is chosen.
if consecutive_lates < 2:
dp[length + 1][total_absences][consecutive_lates + 1] = (
dp[length + 1][total_absences][consecutive_lates + 1] +
dp[length][total_absences][consecutive_lates]
) % MOD
# Sum up the counts for all combinations of length 'n' with different absent and late counts.
count = 0
for total_absences in range(2):
for consecutive_lates in range(3):
count = (count +
dp[n][total_absences][consecutive_lates]) % MOD
return count
Approach 3: Bottom-Up Dynamic Programming, Space Optimized
class Solution:
def checkRecord(self, n: int) -> int:
MOD = 1000000007
# Cache to store current sub-problem results.
dp_curr_state = [[0] * 3 for _ in range(2)]
# Cache to store next sub-problem results.
dp_next_state = [[0] * 3 for _ in range(2)]
# Base case: there is 1 string of length 0 with zero 'A' and zero 'L'.
dp_curr_state[0][0] = 1
# Iterate on smaller sub-problems and use the current smaller sub-problem
# to generate results for bigger sub-problems.
for _ in range(n):
for total_absences in range(2):
for consecutive_lates in range(3):
# Store the count when 'P' is chosen.
dp_next_state[total_absences][0] = (
dp_next_state[total_absences][0] +
dp_curr_state[total_absences][consecutive_lates]
) % MOD
# Store the count when 'A' is chosen.
if total_absences < 1:
dp_next_state[total_absences + 1][0] = (
dp_next_state[total_absences + 1][0] +
dp_curr_state[total_absences][consecutive_lates]
) % MOD
# Store the count when 'L' is chosen.
if consecutive_lates < 2:
dp_next_state[total_absences][consecutive_lates + 1] = (
dp_next_state[total_absences][consecutive_lates + 1] +
dp_curr_state[total_absences][consecutive_lates]
) % MOD
# Next state sub-problems will become current state sub-problems in the next iteration.
dp_curr_state = [row[:] for row in dp_next_state]
# Next state sub-problem results will reset to zero.
dp_next_state = [[0] * 3 for _ in range(2)]
# Sum up the counts for all combinations of length 'n' with different absent and late counts.
count = sum(dp_curr_state[total_absences][consecutive_lates] \
for total_absences in range(2) \
for consecutive_lates in range(3)) % MOD
return count
