Problem of The Day: Time Needed to Buy Tickets

Problem Statement

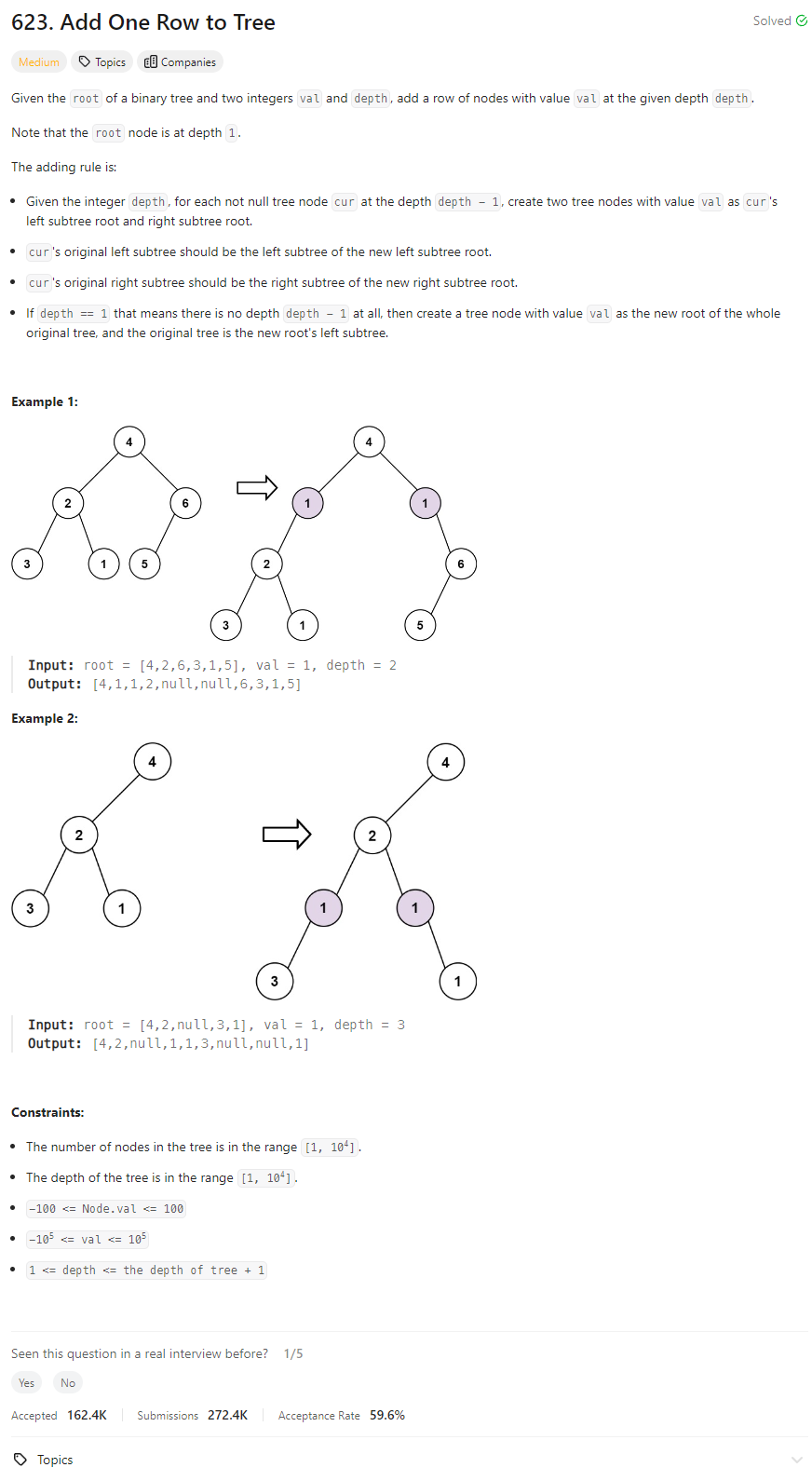
Intuition

My initial thought is to traverse the tree level by level, keeping track of the current depth. When reaching the level just before the target depth, I’ll insert new nodes with the given value as the new row.

Approach

I’ll use a queue to perform a level-order traversal of the binary tree. As I traverse each level, I’ll keep track of the current depth. When I reach the depth just before the target depth, I’ll insert new nodes with the given value as the new row.

Complexity

• Time complexity: O(n) where n is the number of nodes in the binary tree. We need to traverse each node once.

• Space complexity: O(m) where m is the maximum number of nodes at any level in the binary tree. In the worst case, the queue can hold all nodes at the maximum level.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def addOneRow(self, root: Optional[TreeNode], val: int, depth: int) -> Optional[TreeNode]:
        if depth == 1:
            return TreeNode(val, root)
        queue = deque()
        queue.append([root, 1]) # curr, level
        while queue:
            curr, level = queue.popleft()
            if level == depth - 1:
                leftNode = curr.left
                rightNode = curr.right
                curr.left = TreeNode(val, curr.left)
                curr.right = TreeNode(val, None, curr.right)
                continue
            if curr.left:
                queue.append([curr.left, level + 1])
            if curr.right:
                queue.append([curr.right, level + 1])

        return root