Problem of The Day: Smallest Range Covering Elements from K Lists

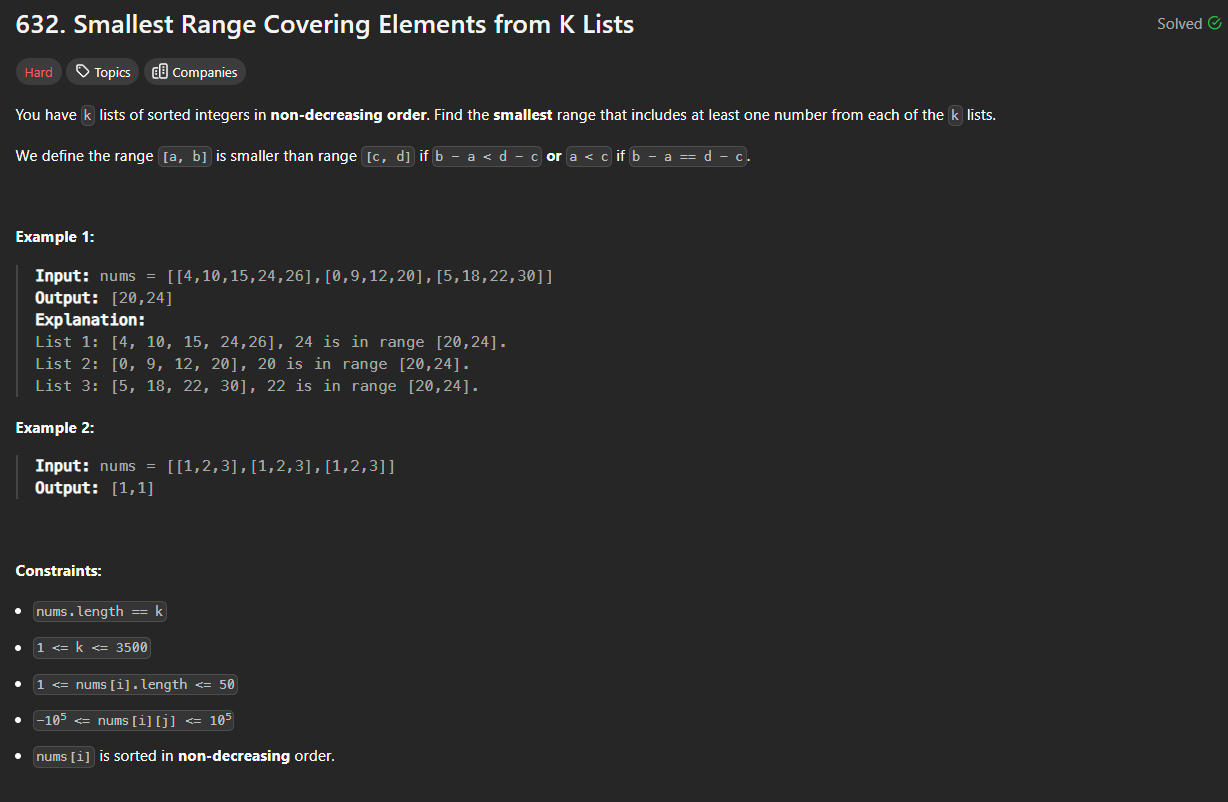
Problem Statement

Brute Force [TLE]

class Solution:
    def smallestRange(self, nums: List[List[int]]) -> List[int]:
        arr = []
        for i, num in enumerate(nums):
            arr.extend([[val, i] for val in num])

        arr.sort(key=lambda x: (x[0], x[1]))

        N = len(arr)
        num_subarrays = len(nums)
        min_length = float('inf')
        res = []
        for i in range(0, N - num_subarrays + 1):
            seen = set()
            j = i
            while j < N:
                seen.add(arr[j][1])
                if len(seen) == num_subarrays:
                    break
                j += 1

            if len(seen) < num_subarrays:
                continue

            curr_length = arr[j][0] - arr[i][0] + 1
            if len(seen) == num_subarrays and min_length > curr_length:
                res = [arr[i][0], arr[j][0]]
                min_length = curr_length

        return res

Editorial

Approach 1: Optimal Brute Force

class Solution:
    def smallestRange(self, nums: List[List[int]]) -> List[int]:
        k = len(nums)
        # Stores the current index of each list
        indices = [0] * k
        # To track the smallest range
        range_list = [0, float("inf")]

        while True:
            cur_min, cur_max = float("inf"), float("-inf")
            min_list_index = 0

            # Find the current minimum and maximum values across the lists
            for i in range(k):
                current_element = nums[i][indices[i]]

                # Update the current minimum
                if current_element < cur_min:
                    cur_min = current_element
                    min_list_index = i

                # Update the current maximum
                if current_element > cur_max:
                    cur_max = current_element

            # Update the range if a smaller one is found
            if cur_max - cur_min < range_list[1] - range_list[0]:
                range_list[0] = cur_min
                range_list[1] = cur_max

            # Move to the next element in the list that had the minimum value
            indices[min_list_index] += 1
            if indices[min_list_index] == len(nums[min_list_index]):
                break

        return range_list

Approach 2: Priority Queue (Heap)

class Solution:
    def smallestRange(self, nums: List[List[int]]) -> List[int]:
        # Priority queue to store (value, list index, element index)
        pq = []
        max_val = float("-inf")
        range_start = 0
        range_end = float("inf")

        # Insert the first element from each list into the min-heap
        for i in range(len(nums)):
            heapq.heappush(pq, (nums[i][0], i, 0))
            max_val = max(max_val, nums[i][0])

        # Continue until we can't proceed further
        while len(pq) == len(nums):
            min_val, row, col = heapq.heappop(pq)

            # Update the smallest range
            if max_val - min_val < range_end - range_start:
                range_start = min_val
                range_end = max_val

            # If possible, add the next element from the same row to the heap
            if col + 1 < len(nums[row]):
                next_val = nums[row][col + 1]
                heapq.heappush(pq, (next_val, row, col + 1))
                max_val = max(max_val, next_val)

        return [range_start, range_end]

Approach 3: Two Pointer

class Solution:
    def smallestRange(self, nums: List[List[int]]) -> List[int]:
        merged = []

        # Merge all lists with their list index
        for i in range(len(nums)):
            for num in nums[i]:
                merged.append((num, i))

        # Sort the merged list
        merged.sort()

        # Two pointers to track the smallest range
        freq = defaultdict(int)
        left, count = 0, 0
        range_start, range_end = 0, float("inf")

        for right in range(len(merged)):
            freq[merged[right][1]] += 1
            if freq[merged[right][1]] == 1:
                count += 1

            # When all lists are represented, try to shrink the window
            while count == len(nums):
                cur_range = merged[right][0] - merged[left][0]
                if cur_range < range_end - range_start:
                    range_start = merged[left][0]
                    range_end = merged[right][0]

                freq[merged[left][1]] -= 1
                if freq[merged[left][1]] == 0:
                    count -= 1
                left += 1

        return [range_start, range_end]

• time: O(n log n)
• space: O(n)