Problem of The Day: Redundant Connection
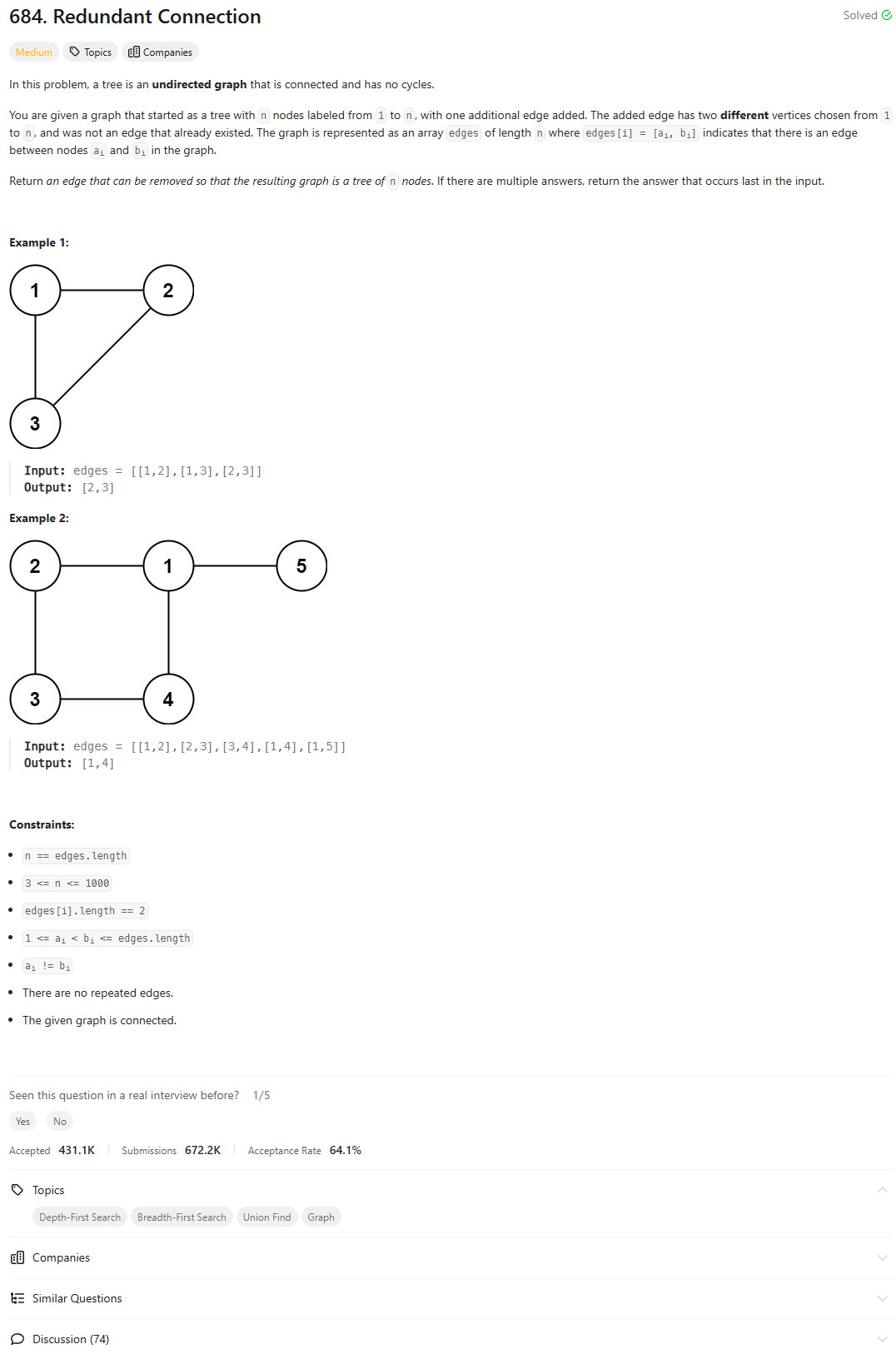
Problem Statement
Intuition
When analyzing the problem, we recognize that we are given a list of edges representing an undirected graph. The task is to determine the edge that, if removed, results in a tree (i.e., a connected acyclic graph). This means that the redundant connection is the edge that creates a cycle in the graph.
A common approach to solving cycle detection problems in an undirected graph is to use the Union-Find (Disjoint Set Union) data structure. This allows us to efficiently track connected components and detect when an edge connects two already connected nodes, thereby forming a cycle.
Approach
-
Initialize Union-Find Data Structure: We create a
UnionFindclass with two main operations:find(x): Recursively finds the root of the component containingx.union(x, y): Merges two components if they are disjoint and returnsTrueif the merge occurs; otherwise, it detects a cycle and returnsFalse.
-
Iterate Through Edges:
- For each edge
[x, y], attempt to unitexandyin the Union-Find structure. - If
union(x, y)returnsTrue, this meansxandywere already connected, forming a cycle. This edge is redundant and should be returned.
- For each edge
-
Handling Edge Cases:
- The algorithm assumes 1-based indexing for the edges, so adjustments are made when accessing Union-Find indices.
- The implementation ensures path compression in
find(x)to optimize future queries, achieving near constant-time complexity per operation.
Complexity
-
Time Complexity:
- Each
findoperation runs in nearly constant time, (inverse Ackermann function). - Since there are at most
nedges, the total time complexity is .
- Each
-
Space Complexity:
- We store parent references (
root) and ranks (rank) fornnodes, leading to space usage.
- We store parent references (
Code
from typing import List
class UnionFind:
def __init__(self, n):
self.root = [i for i in range(n)]
self.rank = [1] * n
def find(self, x):
if x == self.root[x]:
return x
self.root[x] = self.find(self.root[x]) # Path compression
return self.root[x]
def union(self, x, y):
root_x = self.find(x)
root_y = self.find(y)
if root_x == root_y:
return True # Cycle detected
if self.rank[root_x] < self.rank[root_y]:
self.root[root_x] = root_y
elif self.rank[root_x] > self.rank[root_y]:
self.root[root_y] = root_x
else:
self.root[root_y] = root_x
self.rank[root_x] += 1
return False
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
N = len(edges)
uf = UnionFind(N)
for x, y in edges:
if uf.union(x - 1, y - 1): # Adjust for 0-based indexing
return [x, y]
return [] # This should never be reached in a valid input
Editorial
Approach 1: Depth-First Search - Brute Force
class Solution:
# Performs DFS and returns True if there's a path between src and target.
def _is_connected(self, src, target, visited, adj_list):
visited[src] = True
if src == target:
return True
is_found = False
for adj in adj_list[src]:
if not visited[adj]:
is_found = is_found or self._is_connected(
adj, target, visited, adj_list
)
return is_found
def findRedundantConnection(self, edges):
N = len(edges)
adj_list = [[] for _ in range(N)]
for edge in edges:
visited = [False] * N
# If DFS returns True, we will return the edge.
if self._is_connected(edge[0] - 1, edge[1] - 1, visited, adj_list):
return edge
adj_list[edge[0] - 1].append(edge[1] - 1)
adj_list[edge[1] - 1].append(edge[0] - 1)
return []
Approach 2: Depth-First Search - Single Traversal
class Solution:
cycle_start = -1
# Perform the DFS and store a node in the cycle as cycleStart.
def _DFS(self, src, visited, adj_list, parent):
visited[src] = True
for adj in adj_list[src]:
if not visited[adj]:
parent[adj] = src
self._DFS(adj, visited, adj_list, parent)
# If the node is visited and the parent is different then the
# node is part of the cycle.
elif adj != parent[src] and self.cycle_start == -1:
self.cycle_start = adj
parent[adj] = src
def findRedundantConnection(self, edges):
N = len(edges)
visited = [False] * N
parent = [-1] * N
adj_list = [[] for _ in range(N)]
for edge in edges:
adj_list[edge[0] - 1].append(edge[1] - 1)
adj_list[edge[1] - 1].append(edge[0] - 1)
self._DFS(0, visited, adj_list, parent)
cycle_nodes = {}
node = self.cycle_start
# Start from the cycleStart node and backtrack to get all the nodes in
# the cycle. Mark them all in the map.
while True:
cycle_nodes[node] = 1
node = parent[node]
if node == self.cycle_start:
break
# If both nodes of the edge were marked as cycle nodes then this edge
# can be removed.
for i in range(len(edges) - 1, -1, -1):
if (edges[i][0] - 1) in cycle_nodes and (
edges[i][1] - 1
) in cycle_nodes:
return edges[i]
return [] # This line should theoretically never be reached
Approach 3: Disjoint Set Union (DSU)
class DSU:
def __init__(self, N):
# Initialize DSU class, size of each component will be one and each node
# will be representative of its own.
self.N = N
self.size = [1] * N
self.representative = list(range(N))
def _find(self, node):
# Returns the ultimate representative of the node.
if self.representative[node] == node:
return node
self.representative[node] = self._find(self.representative[node])
return self.representative[node]
def _do_union(self, nodeOne, nodeTwo):
# Returns true if node nodeOne and nodeTwo belong to different component and update the
# representatives accordingly, otherwise returns false.
nodeOne = self._find(nodeOne)
nodeTwo = self._find(nodeTwo)
if nodeOne == nodeTwo:
return False
else:
if self.size[nodeOne] > self.size[nodeTwo]:
self.representative[nodeTwo] = nodeOne
self.size[nodeOne] += self.size[nodeTwo]
else:
self.representative[nodeOne] = nodeTwo
self.size[nodeTwo] += self.size[nodeOne]
return True
class Solution:
def findRedundantConnection(self, edges):
N = len(edges)
dsu = DSU(N)
for edge in edges:
# If union returns false, we know the nodes are already connected
# and hence we can return this edge.
if not dsu._do_union(edge[0] - 1, edge[1] - 1):
return edge
return []