Problem of The Day: Magic Squares In Grid
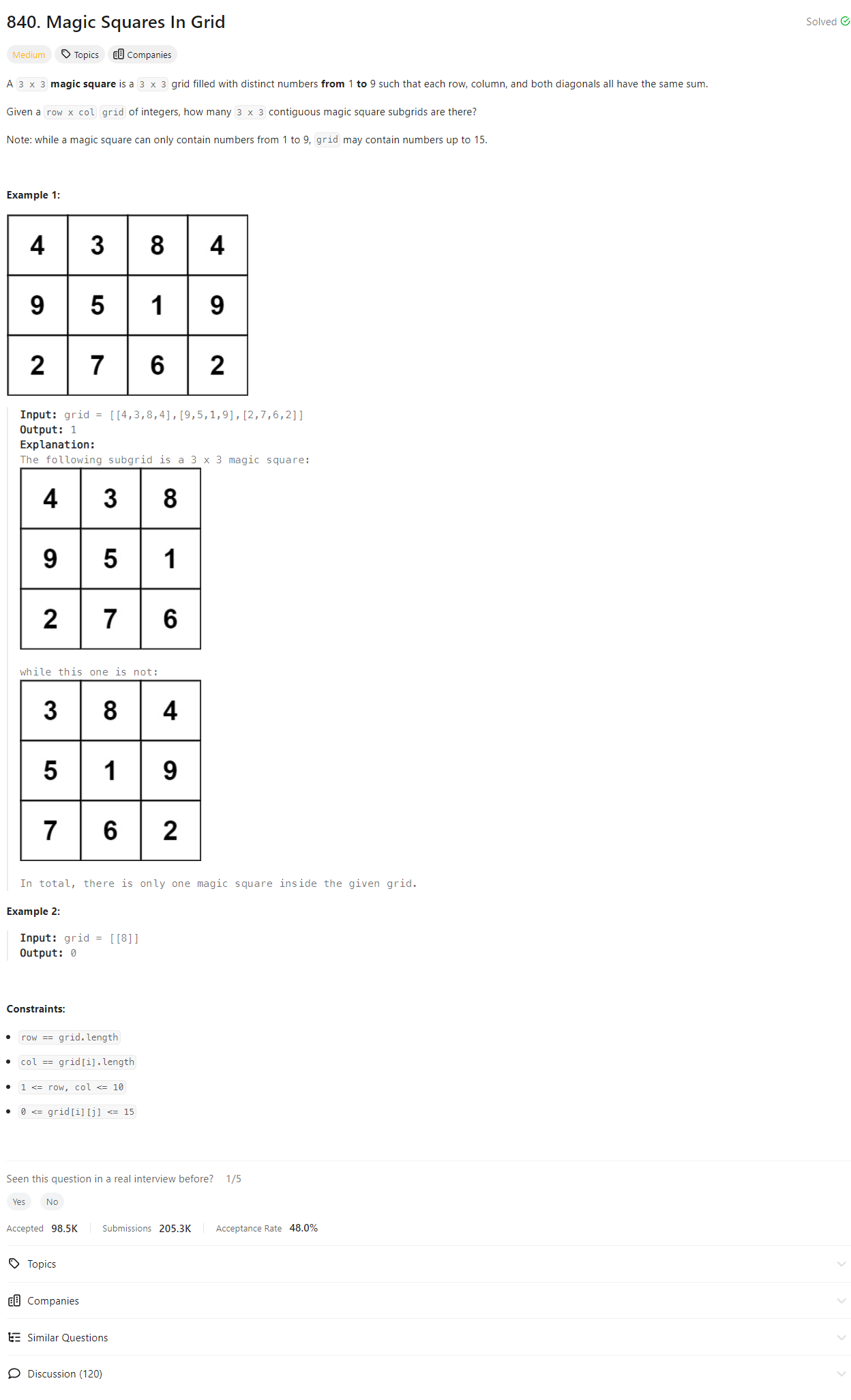
Problem Statement
Brute Force - [Accepted]
Intuition
When I first thought about solving this problem, I realized that the core idea revolves around identifying 3x3 subgrids in a larger grid that qualify as magic squares. A magic square has unique numbers from 1 to 9 and has equal sums for all rows, columns, and diagonals. My approach would involve checking each possible 3x3 grid within the larger grid to see if it meets these criteria.
Approach
To solve the problem, I will iterate through every possible 3x3 subgrid within the given grid. For each subgrid, I will check if it is a magic square by verifying the following:
- Each number in the subgrid is between 1 and 9, and all numbers are unique.
- The sums of all rows, columns, and diagonals are equal.
I will create separate functions to check the validity of rows, columns, and diagonals. If all these checks pass for a subgrid, it will be considered a magic square.
Complexity
- Time complexity: The time complexity is \(O(n^2)\) where
nis the number of rows or columns in the grid. This is because I need to check every possible 3x3 subgrid within the larger grid. - Space complexity: The space complexity is \(O(1)\) because I only use a few additional variables to store sums and sets, and no extra space is required proportional to the input size.
Code
class Solution:
def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
ROWS = len(grid)
COLS = len(grid[0])
def check_cols(r, c):
prev_sum = 0
for col in range(c, c + 3):
curr_sum = 0
seen = set()
for row in range(r, r + 3):
if grid[row][col] >= 10 or grid[row][col] <= 0:
return False
if grid[row][col] in seen:
return False
curr_sum += grid[row][col]
seen.add(grid[row][col])
if prev_sum != 0 and prev_sum != curr_sum:
return False
prev_sum = curr_sum
return True
def check_rows(r, c):
prev_sum = 0
for row in range(r, r + 3):
curr_sum = 0
seen = set()
for col in range(c, c + 3):
if grid[row][col] >= 10 or grid[row][col] <= 0:
return False
if grid[row][col] in seen:
return False
curr_sum += grid[row][col]
seen.add(grid[row][col])
if prev_sum != 0 and prev_sum != curr_sum:
return False
prev_sum = curr_sum
return True
def check_diags(r, c):
l_2_r = 0
row, col = r, c
seen = set()
while row < r + 3 and col < c + 3:
if grid[row][col] >= 10 or grid[row][col] <= 0:
return False
if grid[row][col] in seen:
return False
l_2_r += grid[row][col]
seen.add(grid[row][col])
row += 1
col += 1
r_2_l = 0
row, col = r, c + 2
seen = set()
while row < r + 3 and col >= 0:
if grid[row][col] >= 10 or grid[row][col] <= 0:
return False
if grid[row][col] in seen:
return False
r_2_l += grid[row][col]
seen.add(grid[row][col])
row += 1
col -= 1
return l_2_r == r_2_l
def check_grid(r, c):
if not check_cols(r, c): return False
if not check_rows(r, c): return False
if not check_diags(r, c): return False
return True
res = 0
for row in range(ROWS - 2):
for col in range(COLS - 2):
res += check_grid(row, col)
return res
Editorial
Approach 1: Manual Scan
class Solution:
def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
ans = 0
m = len(grid)
n = len(grid[0])
for row in range(m - 2):
for col in range(n - 2):
if self._isMagicSquare(grid, row, col):
ans += 1
return ans
def _isMagicSquare(self, grid, row, col):
seen = [False] * 10
for i in range(3):
for j in range(3):
num = grid[row + i][col + j]
if num < 1 or num > 9:
return False
if seen[num]:
return False
seen[num] = True
# Check if diagonal sums are the same
diagonal1 = (
grid[row][col] + grid[row + 1][col + 1] + grid[row + 2][col + 2]
)
diagonal2 = (
grid[row + 2][col] + grid[row + 1][col + 1] + grid[row][col + 2]
)
if diagonal1 != diagonal2:
return False
# Check if all row sums are the same as the diagonal sums
row1 = grid[row][col] + grid[row][col + 1] + grid[row][col + 2]
row2 = (
grid[row + 1][col] + grid[row + 1][col + 1] + grid[row + 1][col + 2]
)
row3 = (
grid[row + 2][col] + grid[row + 2][col + 1] + grid[row + 2][col + 2]
)
if not (row1 == diagonal1 and row2 == diagonal1 and row3 == diagonal1):
return False
# Check if all column sums are the same as the diagonal sums
col1 = grid[row][col] + grid[row + 1][col] + grid[row + 2][col]
col2 = (
grid[row][col + 1] + grid[row + 1][col + 1] + grid[row + 2][col + 1]
)
col3 = (
grid[row][col + 2] + grid[row + 1][col + 2] + grid[row + 2][col + 2]
)
if not (col1 == diagonal1 and col2 == diagonal1 and col3 == diagonal1):
return False
return True
Approach 2: Check Unique Properties of Magic Square
class Solution:
def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
ans = 0
m = len(grid)
n = len(grid[0])
for row in range(m - 2):
for col in range(n - 2):
if self._isMagicSquare(grid, row, col):
ans += 1
return ans
def _isMagicSquare(self, grid, row, col):
# The sequences are each repeated twice to account for
# the different possible starting points of the sequence
# in the magic square
sequence = "2943816729438167"
sequenceReversed = "7618349276183492"
border = []
# Flattened indices for bordering elements of 3x3 grid
borderIndices = [0, 1, 2, 5, 8, 7, 6, 3]
for i in borderIndices:
num = grid[row + i // 3][col + (i % 3)]
border.append(str(num))
borderConverted = "".join(border)
# Make sure the sequence starts at one of the corners
return (
grid[row][col] % 2 == 0
and (
sequence.find(borderConverted) != -1
or sequenceReversed.find(borderConverted) != -1
)
and grid[row + 1][col + 1] == 5
)