Problem of The Day: Sum of Distances in Tree

Problem Statement

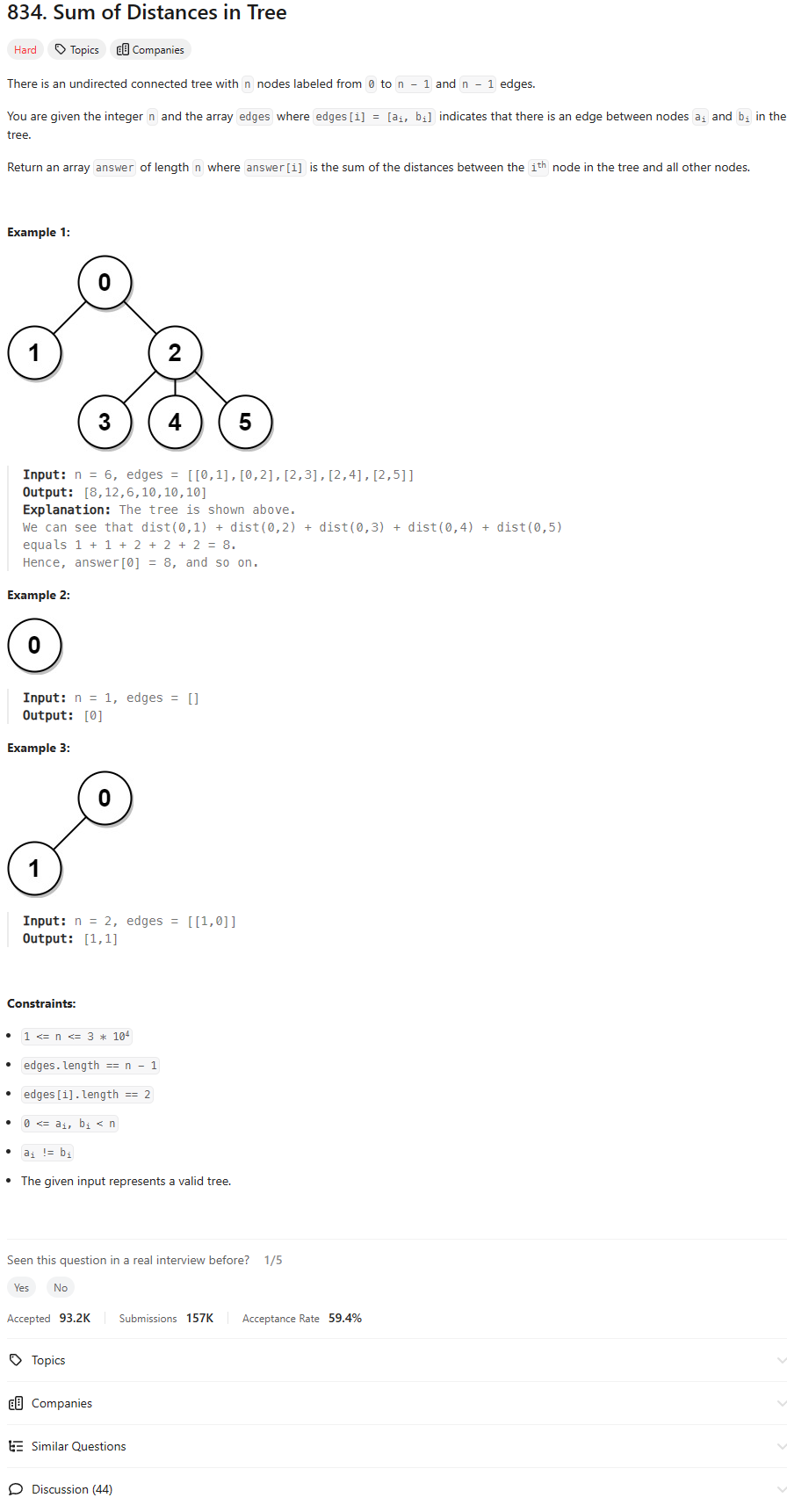
Notes:

• Need to review this problem again.

BFS Approach - TLE

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        graph = {i: [] for i in range(n)}
        for a,b in edges:
            graph[a].append(b)
            graph[b].append(a)

        def bfs(i):
            queue = deque()
            queue.append([i, 0])
            visited = {i}
            total_dist = 0
            while queue:
                node, dist = queue.popleft()
                total_dist += dist
                for nei in graph[node]:
                    if nei not in visited:
                        queue.append([nei, dist + 1])
                        visited.add(nei)
            return total_dist

        res = []
        for i in range(n):
            res.append(bfs(i))
        return res

Editorial Solution

class Solution(object):
    def sumOfDistancesInTree(self, N, edges):
        graph = collections.defaultdict(set)
        for u, v in edges:
            graph[u].add(v)
            graph[v].add(u)

        count = [1] * N
        ans = [0] * N
        def dfs(node = 0, parent = None):
            for child in graph[node]:
                if child != parent:
                    dfs(child, node)
                    count[node] += count[child]
                    ans[node] += ans[child] + count[child]

        def dfs2(node = 0, parent = None):
            for child in graph[node]:
                if child != parent:
                    ans[child] = ans[node] - count[child] + N - count[child]
                    dfs2(child, node)

        dfs()
        dfs2()
        return ans

• Time: O(n)
• Space: O(n)