Software Engineer

2 minute read

Problem Statement

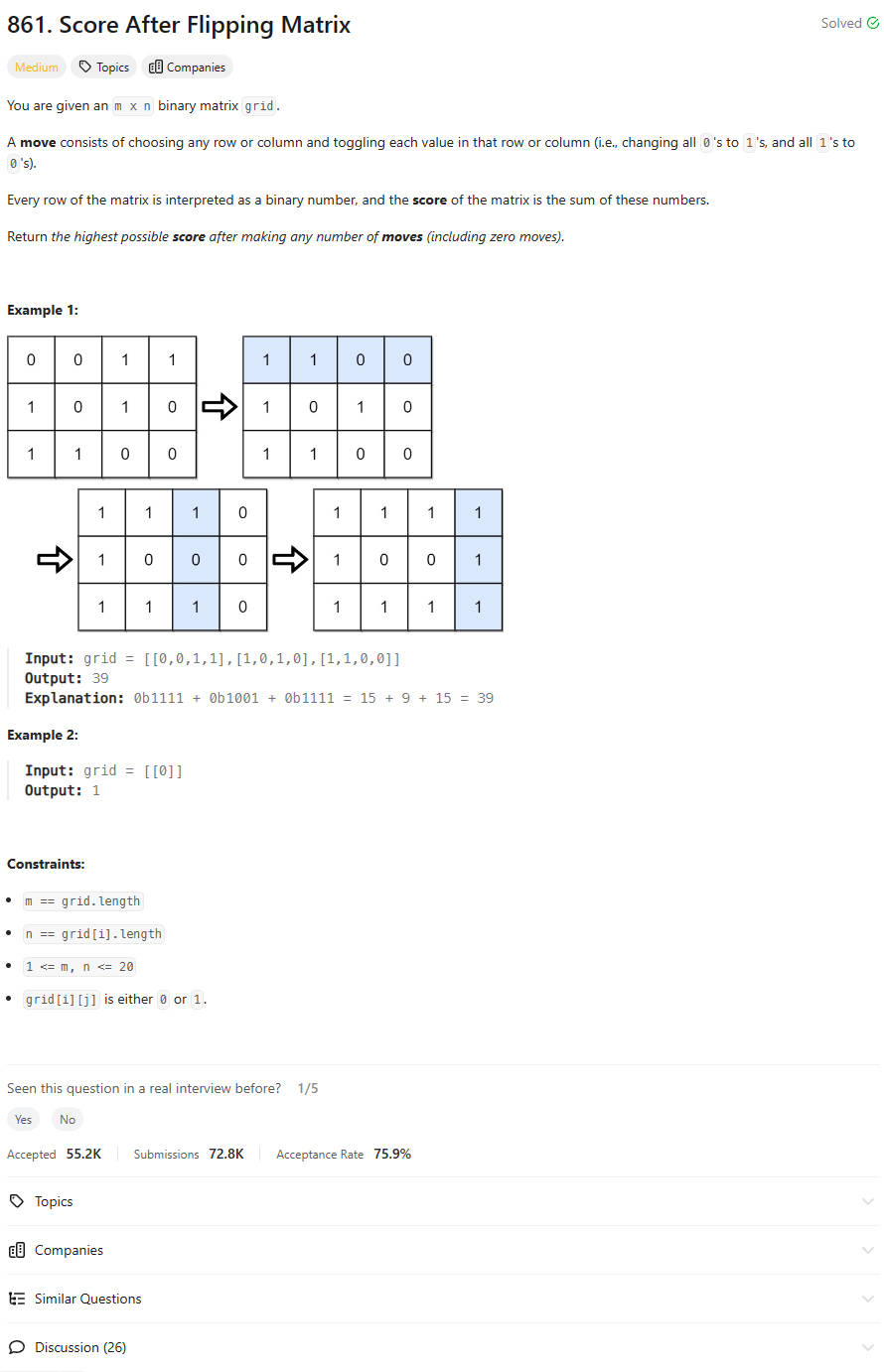
problem-861

Intuition

The problem seems to revolve around maximizing the score of a binary matrix by toggling rows and columns.

Approach

My initial thought is to approach this problem iteratively. First, I’ll focus on making all the first elements of each row to be 1, since that would give the maximum possible value for that bit. Then, I’ll iterate through each column and toggle it if the number of 0s is greater than the number of 1s.

Complexity

  • Time complexity: O(m * n)

  • Space complexity: O(1)

Code

class Solution:
    def matrixScore(self, grid: List[List[int]]) -> int:
        rows = len(grid)
        cols = len(grid[0])

        def toggle_value_row(row):
            for col in range(cols):
                grid[row][col] = 0 if grid[row][col] == 1 else 1

        def toggle_value_col(col):
            for row in range(rows):
                grid[row][col] = 0 if grid[row][col] == 1 else 1

        for row in range(rows):
            for col in range(cols):
                if grid[row][col] == 1:
                    break
                if grid[row][col] == 0:
                    toggle_value_row(row)
                    break


        for col in range(cols):
            counter = Counter()
            for row in range(rows):
                counter[grid[row][col]] += 1

            if counter[0] > counter[1]:
                toggle_value_col(col)

        res = 0
        for row in range(rows):
            i = 0
            for col in reversed(range(cols)):
                if grid[row][col] == 1:
                    res += (2 ** i)
                i += 1
        return res

Editorial Solution

Approach 1: Greedy Way (Modifying Input)

class Solution:
    def matrixScore(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])

        # Set first column
        for i in range(m):
            if grid[i][0] == 0:
                # Flip row
                for j in range(n):
                    grid[i][j] = 1 - grid[i][j]  # Bitwise XOR for flip

        # Optimize columns except first column
        for j in range(1, n):
            count_zero = 0
            # Count zeros
            for i in range(m):
                if grid[i][j] == 0:
                    count_zero += 1
            # Flip the column if more zeros for better score
            if count_zero > m - count_zero:
                for i in range(m):
                    grid[i][j] ^= 1  # Bitwise XOR for flip

        # Calculate the final score considering bit positions
        score = 0
        for i in range(m):
            for j in range(n):
                # Left shift bit by place value of column to find column contribution
                columnScore = grid[i][j] << (n - j - 1)
                # Add contribution to score
                score += columnScore

        # Return final result
        return score

Approach 2: Greedy Way (Without Modifying Input)

class Solution:
    def matrixScore(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])

        # Set score to summation of first column
        score = (1 << (n - 1)) * m

        # Loop over all other columns
        for j in range(1, n):
            count_same_bits = 0
            for i in range(m):
                # Count elements matching first in row
                if grid[i][j] == grid[i][0]:
                    count_same_bits += 1

            # Calculate score based on the number of same bits in a column
            count_same_bits = max(count_same_bits, m - count_same_bits)
            # Calculate the score contribution for the current column
            column_score = (1 << (n - j - 1)) * count_same_bits
            # Add contribution to score
            score += column_score

        return score

You may also enjoy