Problem of The Day: Regions Cut By Slashes
Problem Statement

Notes:
- This is difficult medium problem. Need to review.
- Can review the Number of Island problem to solve using DFS/BFS
Intuition
The problem can be visualized as splitting each cell of the grid into smaller parts based on the slashes. We can think of each cell as having four parts and depending on the slash, we will connect certain parts within the cell or with adjacent cells. The DSU (Disjoint Set Union) structure is a natural fit for managing these connections and counting the number of regions.
Approach
- Treat each cell in the grid as divided into four triangles.
- Use a DSU to manage these triangles.
- For each cell, depending on the slash or space, connect the appropriate triangles.
- Also, connect triangles between adjacent cells to form the regions.
- Finally, count the number of distinct regions by counting the number of unique sets in the DSU.
Complexity
-
Time complexity: The time complexity is \(O(N^2)\) where
Nis the size of the grid. This is because we process each cell and perform union-find operations which are almost constant in time due to path compression. -
Space complexity: The space complexity is also \(O(N^2)\) because we are using a DSU structure to store the parent of each part of each cell.
Code
class DSU:
def __init__(self, N):
self.p = list(range(N))
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, x, y):
xr = self.find(x)
yr = self.find(y)
self.p[xr] = yr
class Solution(object):
def regionsBySlashes(self, grid):
N = len(grid)
dsu = DSU(4 * N * N)
for r, row in enumerate(grid):
for c, val in enumerate(row):
root = 4 * (r*N + c)
if val in '/ ':
dsu.union(root + 0, root + 1)
dsu.union(root + 2, root + 3)
if val in '\ ':
dsu.union(root + 0, root + 2)
dsu.union(root + 1, root + 3)
# north/south
if r+1 < N: dsu.union(root + 3, (root+4*N) + 0)
if r-1 >= 0: dsu.union(root + 0, (root-4*N) + 3)
# east/west
if c+1 < N: dsu.union(root + 2, (root+4) + 1)
if c-1 >= 0: dsu.union(root + 1, (root-4) + 2)
return sum(dsu.find(x) == x for x in range(4*N*N))
Editorial
Approach 1: Expanded Grid
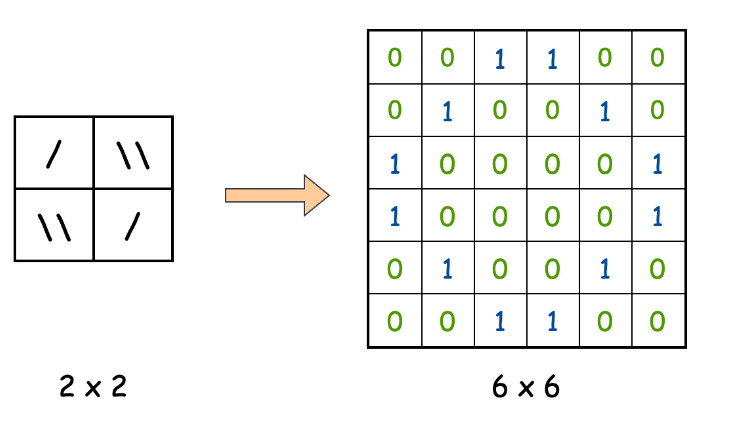
class Solution:
# Directions for traversal: right, left, down, up
DIRECTIONS = [
(0, 1),
(0, -1),
(1, 0),
(-1, 0),
]
def regionsBySlashes(self, grid):
grid_size = len(grid)
# Create a 3x3 matrix for each cell in the original grid
expanded_grid = [[0] * (grid_size * 3) for _ in range(grid_size * 3)]
# Populate the expanded grid based on the original grid
# 1 represents a barrier in the expanded grid
for i in range(grid_size):
for j in range(grid_size):
base_row = i * 3
base_col = j * 3
# Check the character in the original grid
if grid[i][j] == "\\":
# Mark diagonal for backslash
expanded_grid[base_row][base_col] = 1
expanded_grid[base_row + 1][base_col + 1] = 1
expanded_grid[base_row + 2][base_col + 2] = 1
elif grid[i][j] == "/":
# Mark diagonal for forward slash
expanded_grid[base_row][base_col + 2] = 1
expanded_grid[base_row + 1][base_col + 1] = 1
expanded_grid[base_row + 2][base_col] = 1
region_count = 0
# Count regions using flood fill
for i in range(grid_size * 3):
for j in range(grid_size * 3):
# If we find an unvisited cell (0), it's a new region
if expanded_grid[i][j] == 0:
# Fill that region
self._flood_fill(expanded_grid, i, j)
region_count += 1
return region_count
# Flood fill algorithm to mark all cells in a region
def _flood_fill(self, expanded_grid, row, col):
queue = [(row, col)]
expanded_grid[row][col] = 1
while queue:
current_cell = queue.pop(0)
# Check all four directions from the current cell
for direction in self.DIRECTIONS:
new_row = direction[0] + current_cell[0]
new_col = direction[1] + current_cell[1]
# If the new cell is valid and unvisited, mark it and add to queue
if self._is_valid_cell(expanded_grid, new_row, new_col):
expanded_grid[new_row][new_col] = 1
queue.append((new_row, new_col))
# Check if a cell is within bounds and unvisited
def _is_valid_cell(self, expanded_grid, row, col):
n = len(expanded_grid)
return (
row >= 0
and col >= 0
and row < n
and col < n
and expanded_grid[row][col] == 0
)
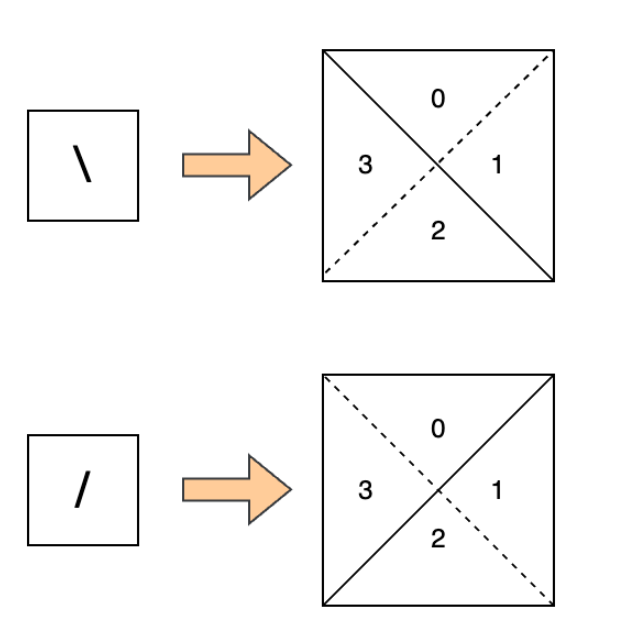
Approach 2: Disjoint Set Union (Triangles)
The idea is to envision each cell divided into four triangles. Then use Disjoint Set Union (DSU) to solve the problem
class Solution:
def regionsBySlashes(self, grid: List[str]) -> int:
grid_size = len(grid)
total_triangles = grid_size * grid_size * 4
parent_array = [-1] * total_triangles
# Initially, each small triangle is a separate region
region_count = total_triangles
for row in range(grid_size):
for col in range(grid_size):
# Connect with the cell above
if row > 0:
region_count -= self._union_triangles(
parent_array,
self._get_triangle_index(grid_size, row - 1, col, 2),
self._get_triangle_index(grid_size, row, col, 0),
)
# Connect with the cell to the left
if col > 0:
region_count -= self._union_triangles(
parent_array,
self._get_triangle_index(grid_size, row, col - 1, 1),
self._get_triangle_index(grid_size, row, col, 3),
)
# If not '/', connect triangles 0-1 and 2-3
if grid[row][col] != "/":
region_count -= self._union_triangles(
parent_array,
self._get_triangle_index(grid_size, row, col, 0),
self._get_triangle_index(grid_size, row, col, 1),
)
region_count -= self._union_triangles(
parent_array,
self._get_triangle_index(grid_size, row, col, 2),
self._get_triangle_index(grid_size, row, col, 3),
)
# If not '\', connect triangles 0-3 and 1-2
if grid[row][col] != "\\":
region_count -= self._union_triangles(
parent_array,
self._get_triangle_index(grid_size, row, col, 0),
self._get_triangle_index(grid_size, row, col, 3),
)
region_count -= self._union_triangles(
parent_array,
self._get_triangle_index(grid_size, row, col, 2),
self._get_triangle_index(grid_size, row, col, 1),
)
return region_count
# Calculate the index of a triangle in the flattened array
# Each cell is divided into 4 triangles, numbered 0 to 3 clockwise from the top
def _get_triangle_index(self, grid_size, row, col, triangle_num):
return (grid_size * row + col) * 4 + triangle_num
# Union two triangles and return 1 if they were not already connected, 0 otherwise
def _union_triangles(self, parent_array, x, y):
parent_x = self._find_parent(parent_array, x)
parent_y = self._find_parent(parent_array, y)
if parent_x != parent_y:
parent_array[parent_x] = parent_y
return 1 # Regions were merged, so count decreases by 1
return 0 # Regions were already connected
# Find the parent (root) of a set
def _find_parent(self, parent_array, x):
if parent_array[x] == -1:
return x
parent_array[x] = self._find_parent(parent_array, parent_array[x])
return parent_array[x]