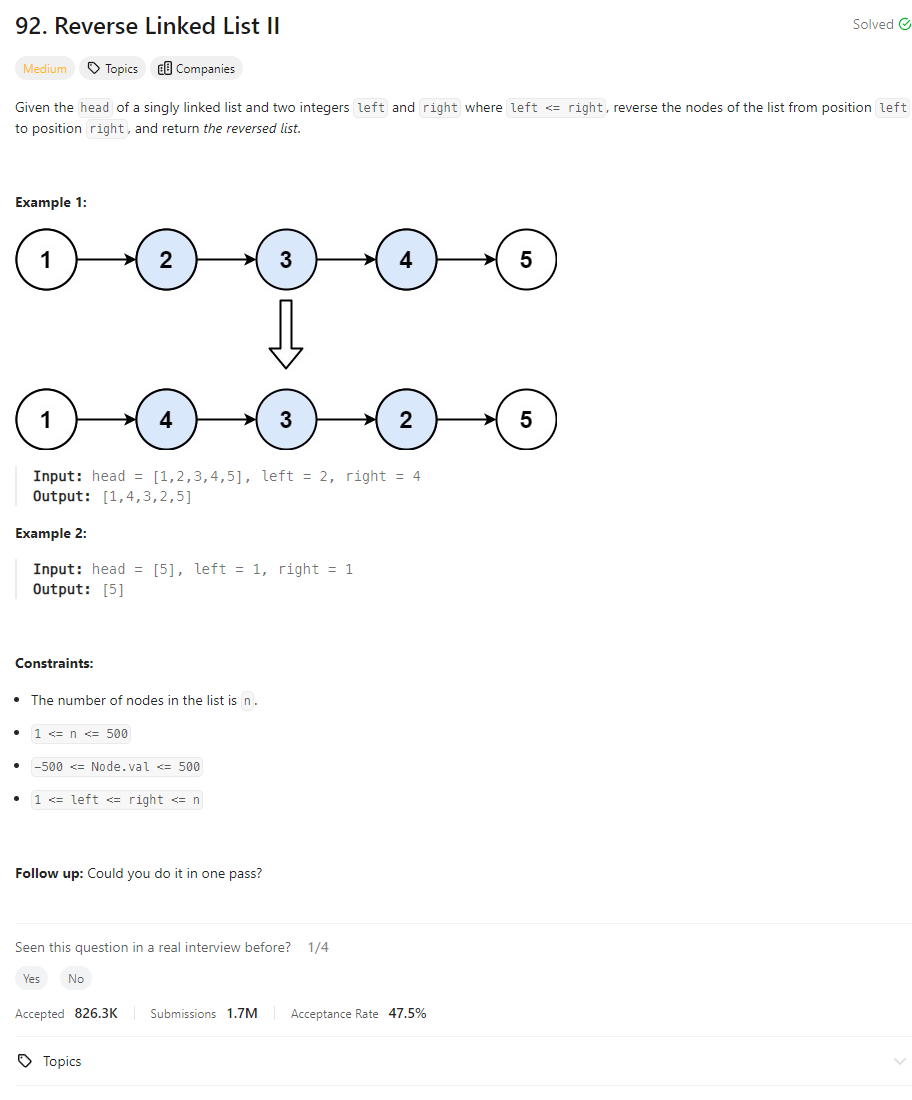
Problem of The Day: Reverse Linked List II

Problem Statement

Intuition

My initial thoughts are to traverse the list until the specified range, reverse that portion, and then connect it back to the original list.

Approach

I will use two pointers, prev and curr, to traverse the linked list until I reach the node at index left. At this point, I’ll start reversing the nodes until I reach the node at index right. I’ll also keep track of the nodes before and after the reversed portion. Finally, I’ll connect these nodes appropriately to ensure the reversed portion is integrated back into the original list.

Complexity

• Time complexity: O(n)

• Space complexity: O(1)

Code

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseBetween(self, head: Optional[ListNode], left: int, right: int) -> Optional[ListNode]:
        if left is right:
            return head
        dummy = ListNode(-1, head)
        prev_left = curr = head
        left_node = right_node = None
        prev = dummy
        next_right = None
        count = 1

        while curr:
            if count == left:
                left_node = curr
                prev_left = prev
            if count == right:
                right_node = curr
                next_right = curr.next

            prev = curr
            curr = curr.next
            count += 1

        prev = None
        curr = left_node
        right_node.next = None
        while curr is not None:
            next_node = curr.next
            curr.next = prev
            prev = curr
            curr = next_node

        prev_left.next, left_node.next = right_node, next_right

        return dummy.next

Editorial Solution

Approach 1: Recursion

class Solution:
    def reverseBetween(self, head, m, n):
        """
        :type head: ListNode
        :type m: int
        :type n: int
        :rtype: ListNode
        """

        if not head:
            return None

        left, right = head, head
        stop = False
        def recurseAndReverse(right, m, n):
            nonlocal left, stop

            # base case. Don't proceed any further
            if n == 1:
                return

            # Keep moving the right pointer one step forward until (n == 1)
            right = right.next

            # Keep moving left pointer to the right until we reach the proper node
            # from where the reversal is to start.
            if m > 1:
                left = left.next

            # Recurse with m and n reduced.
            recurseAndReverse(right, m - 1, n - 1)

            # In case both the pointers cross each other or become equal, we
            # stop i.e. don't swap data any further. We are done reversing at this
            # point.
            if left == right or right.next == left:
                stop = True

            # Until the boolean stop is false, swap data between the two pointers
            if not stop:
                left.val, right.val = right.val, left.val

                # Move left one step to the right.
                # The right pointer moves one step back via backtracking.
                left = left.next

        recurseAndReverse(right, m, n)
        return head

• Time complexity: O(n)
• Space complexity: O(n)

Approach 2: Iterative Link Reversal

class Solution:
    def reverseBetween(self, head, m, n):
        """
        :type head: ListNode
        :type m: int
        :type n: int
        :rtype: ListNode
        """

        # Empty list
        if not head:
            return None

        # Move the two pointers until they reach the proper starting point
        # in the list.
        cur, prev = head, None
        while m > 1:
            prev = cur
            cur = cur.next
            m, n = m - 1, n - 1

        # The two pointers that will fix the final connections.
        tail, con = cur, prev

        # Iteratively reverse the nodes until n becomes 0.
        while n:
            third = cur.next
            cur.next = prev
            prev = cur
            cur = third
            n -= 1

        # Adjust the final connections as explained in the algorithm
        if con:
            con.next = prev
        else:
            head = prev
        tail.next = cur
        return head

• Time complexity: O(n)
• Space complexity: O(1)