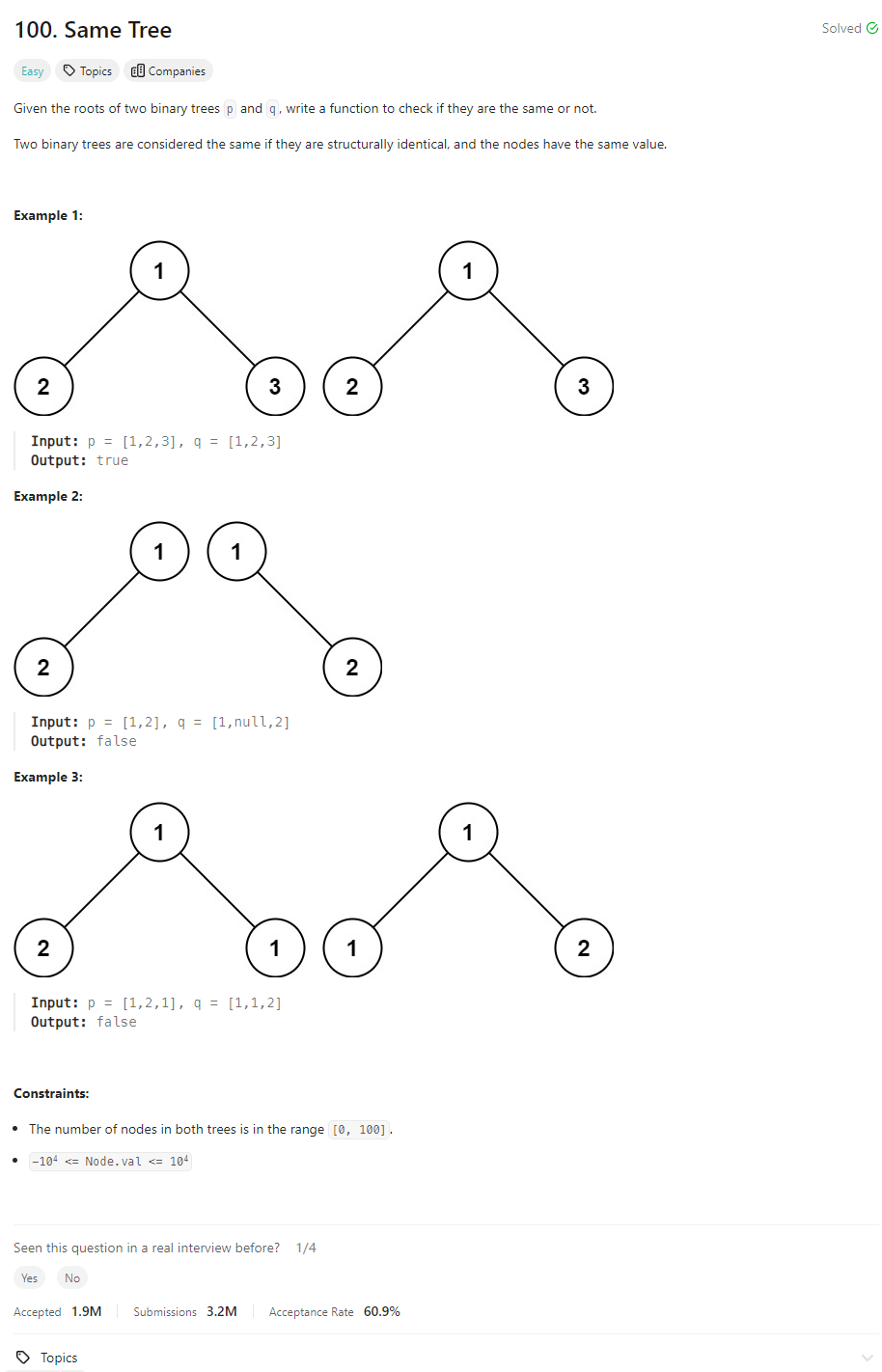
Problem of The Day: Same Tree

Problem Statement

Intuition

My initial thought is to perform a preorder traversal on both trees and compare the resulting traversal lists. If the traversal lists of both trees are the same, then the trees are identical.

Approach

I will use a recursive approach to perform a preorder traversal on both trees. During the traversal, I will append the values of the nodes to separate lists for each tree. If a node is None, I will append a special marker (such as None) to indicate the absence of a node at that position. After the traversal, I will compare the lists for both trees. If the lists are equal, the trees are identical.

Complexity

• Time complexity: O(n) where n is the number of nodes in the larger of the two trees. This is because we traverse each node once.

• Space complexity: O(n) where n is the number of nodes in the larger of the two trees. This is because we store the values of all nodes in lists during traversal.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        def preorder_travesal(node, curr):
            if not node:
                curr.append(None)
                return

            curr.append(node.val)
            preorder_travesal(node.left, curr)
            preorder_travesal(node.right, curr)

        p_list, q_list = [], []
        preorder_travesal(p, p_list)
        preorder_travesal(q, q_list)
        return p_list == q_list

Alternative Approach

Instead of traversing the two trees twice and storing the two lists, we can traverse the two trees simultaneously and check for valid conditions at each step, as demonstrated below.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if not p and not q:
            return True
        if p and not q:
            return False
        if not p and q:
            return False
        if p.val != q.val:
            return False
        return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

• Time complexity: O(n)
• Space complexity: O(n)