Problem of The Day: Trapping Rain Water

Problem Statement

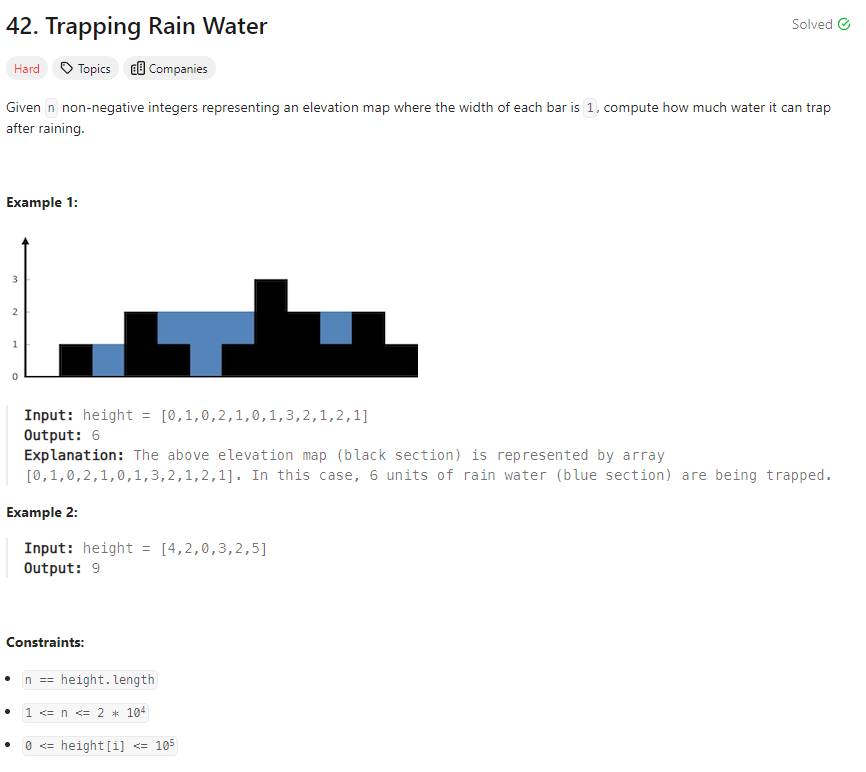
I attempted to solve this problem using monotonic approach. For other approaches, please see this Journal.

My note:

Index (end)	Current Height	Stack	Water Trapped
0	0	[0]	0
1	1	[1]	0
2	0	[1, 2]	1
3	2	[3]	0
4	1	[3, 4]	0
5	0	[3, 4, 5]	1
6	1	[3, 4, 6]	0
7	3	[7]	0
8	2	[7, 8]	0
9	1	[7, 9]	1
10	2	[7, 10]	2
11	1	[7, 10, 11]	0

total water = 1 + 1 + 1 + 2 = 6

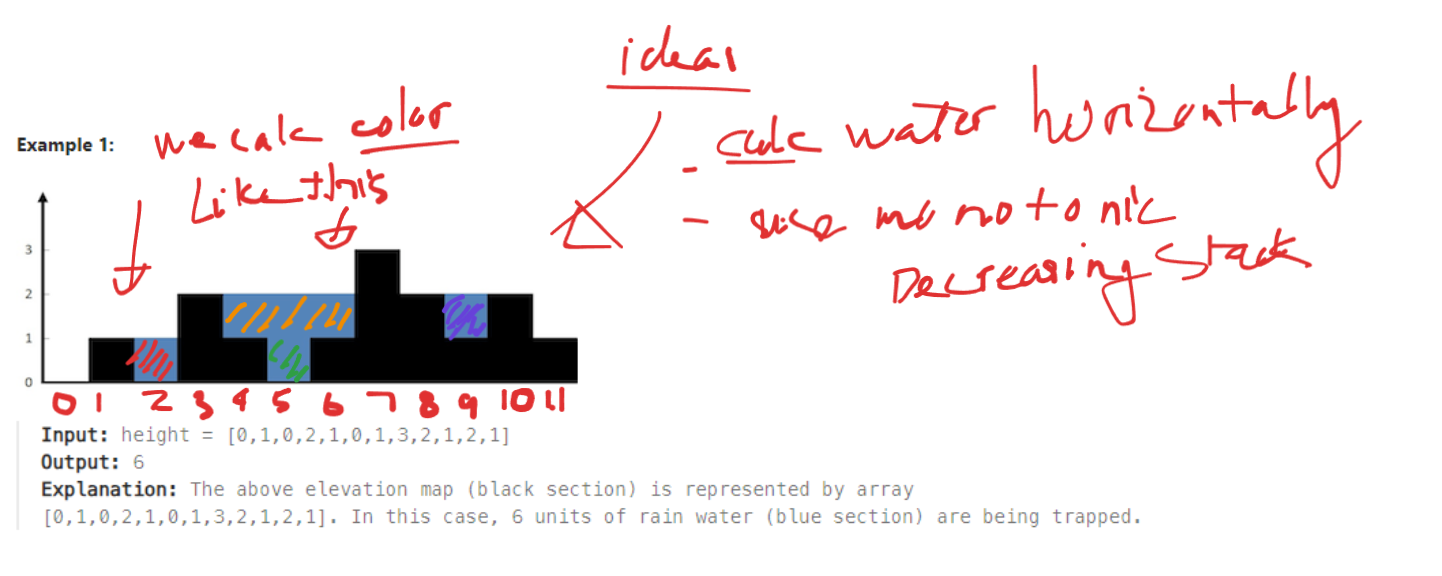
Intuition

The intuition behind this solution is to use a monotonic decreasing stack to keep track of the indices of the heights in the array. The stack helps in identifying the potential boundaries of a trapped water region. The idea is to iterate through the array, and for each element, check whether it can form a trapped water region with the previous elements in the stack.

Approach

• Initialize an empty stack to keep track of indices.
• Iterate through the array, and for each element:
  • While the stack is not empty and the current height is greater than the height at the index on the top of the stack:
    • Pop the index from the stack (let’s call it j).
    • If the stack is not empty, calculate the trapped water between the current index (end) and the index on top of the stack (start).
      • Calculate the height of the trapped water as the minimum of the current height and the height at the index on top of the stack, minus the height at index j.
      • Calculate the width of the trapped water region as the difference between the current index (end) and the index on top of the stack (start), minus 1.
      • Add the calculated water volume to the total water.
  • Push the current index (end) onto the stack.
• Return the total trapped water.

Complexity

• Time complexity: O(n) - The algorithm iterates through the array once.

• Space complexity: O(n) - In the worst case, the stack can store all elements of the array.

Code

class Solution:
    def trap(self, height: List[int]) -> int:
        stack = []
        curr_max = 0
        water = 0
        for end, curr_height in enumerate(height):
            while stack and height[stack[-1]] < curr_height:
                j = stack.pop()
                if stack:
                    start = stack[-1]
                    height_start = height[start]
                    h = min(curr_height, height_start) - height[j]
                    d = end - start - 1
                    water += (d * h)
            stack.append(end)
        return water