Problem of The Day: Minimum Cost to Buy Apples

Problem Statement

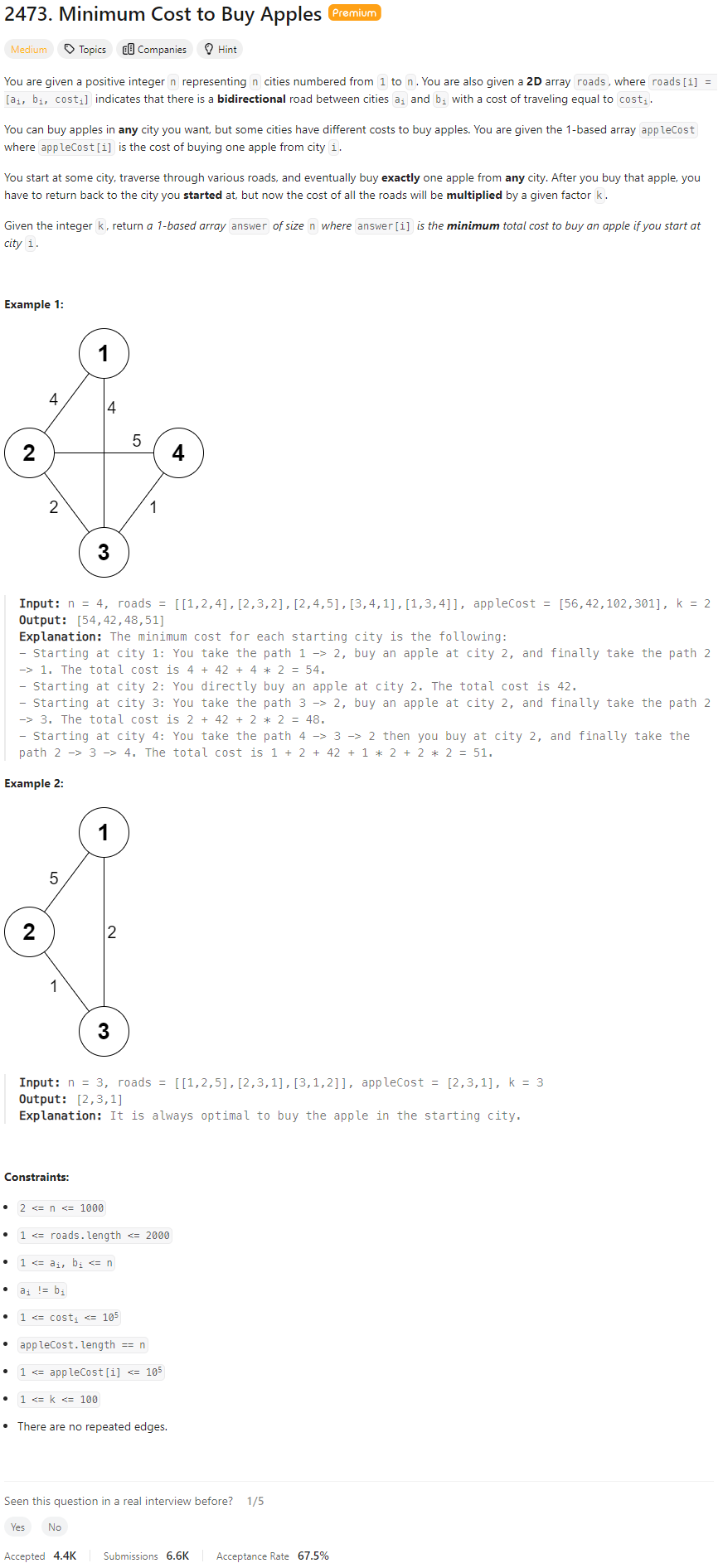
• Note: need to review the Dijkstra’s algorithm to solve the problem

Backtrack Approach - TLE

class Solution:
    def minCost(self, n: int, roads: List[List[int]], appleCost: List[int], k: int) -> List[int]:
        res = [float('inf')] * n
        graph = {i: [] for i in range(1, n + 1)}
        for x, y, cost in roads:
            graph[x].append([y, cost])
            graph[y].append([x, cost])

        minCost = min(appleCost)
        dest = appleCost.index(minCost) + 1

        def dfs(index):
            if index == dest:
                return appleCost[index - 1]

            ans = float('inf')
            for nei, cost in graph[index]:
                if nei not in visited:
                    visited.add(nei)
                    ans = min(ans, dfs(nei) + cost + k * cost, appleCost[index - 1])
                    visited.remove(nei)
            return ans

        for i in range(1, n + 1):
            visited = set()
            visited.add(i)
            res[i - 1] = dfs(i)
        return res

Editorial Solution

Approach 1: Shortest Path

Apply modified Dijkstra’s algorithm to solve the problem

class Solution:
    def minCost(
        self, n: int, roads: List[List[int]], appleCost: List[int], k: int
    ) -> List[int]:
        # Store the graph as a list of lists
        # The rows represent the cities (vertices)
        # The columns store an adjacency list of road, cost pairs (edge, weight)
        graph = [[] for _ in range(n)]

        # Add each road to the graph using adjacency lists
        # Store each city at `graph[city - 1]`
        for city_a, city_b, cost in roads:
            graph[city_a - 1].append((city_b - 1, cost))
            graph[city_b - 1].append((city_a - 1, cost))

        # Finds the minimum cost to buy an apple from the start city
        def shortest_path(start_city, graph):
            # Stores the travel cost reach each city from the start city
            travel_costs = [float("inf") for _ in range(n)]
            travel_costs[start_city] = 0

            # Initialize the heap (priority queue) with the starting city
            # Each element of the heap is a tuple with the cost and city
            heap = [(0, start_city)]
            min_cost = float("inf")

            while heap:
                # Remove the city with the minimum cost from the top of the heap
                travel_cost, curr_city = heapq.heappop(heap)

                # Update the min cost if the curr city has a smaller total cost
                min_cost = min(min_cost,
                               appleCost[curr_city] + (k + 1) * travel_cost)

                # Add each neighboring city to the heap if an apple is cheaper
                for neighbor, cost in graph[curr_city]:
                    next_cost = travel_cost + cost
                    if next_cost < travel_costs[neighbor]:
                        travel_costs[neighbor] = next_cost
                        heapq.heappush(heap, (next_cost, neighbor))

            return min_cost

        # Find the minimum cost to buy an apple starting in each city
        ans = []
        for start_city in range(0, n):
            ans.append(shortest_path(start_city, graph))

        return ans

• Time: O(n _ (n + r) _ log n)
• Space: O(n + r)

Approach 2: One Pass Shortest Path

class Solution:
    def minCost(
        self, n: int, roads: List[List[int]], appleCost: List[int], k: int
    ) -> List[int]:
        # Store the graph as a list of lists
        # The rows represent the cities (vertices)
        # The columns store an adjacency list of road, cost pairs (edge, weight)
        graph = [[] for _ in range(n)]

        # Add each road to the graph using adjacency lists
        # Store each city at `graph[city - 1]`
        for city_a, city_b, cost in roads:
            graph[city_a - 1].append((city_b - 1, cost))
            graph[city_b - 1].append((city_a - 1, cost))

        # Store the cost to buy an apple in each city
        # without traveling in the result
        result = list(appleCost)

        # Initialize the min heap (priority queue) with each starting city
        # Each element of the heap is a tuple with the cost and city
        heap = [(apple_cost, start_city)
                 for start_city, apple_cost in enumerate(appleCost)]
        heapify(heap)

        # Find the minimum cost to buy an apple starting in each city
        while heap:
            # Remove the city with the minimum cost from the top of the heap
            total_cost, curr_city = heapq.heappop(heap)

            # If we have already found a path to buy an apple
            # for cheaper than the local apple cost, skip this city
            if result[curr_city] < total_cost:
                continue

            # Add each neighboring city to the heap if it is cheaper to
            # start there, travel to the current city and buy an apple
            # than buy in the neighboring city
            for neighbor, cost in graph[curr_city]:
                if result[neighbor] > result[curr_city] + (k + 1) * cost:
                    result[neighbor] = result[curr_city] + (k + 1) * cost
                    heapq.heappush(heap, (result[neighbor], neighbor))

        return result