Problem of The Day: Path with Maximum Gold

Problem Statement

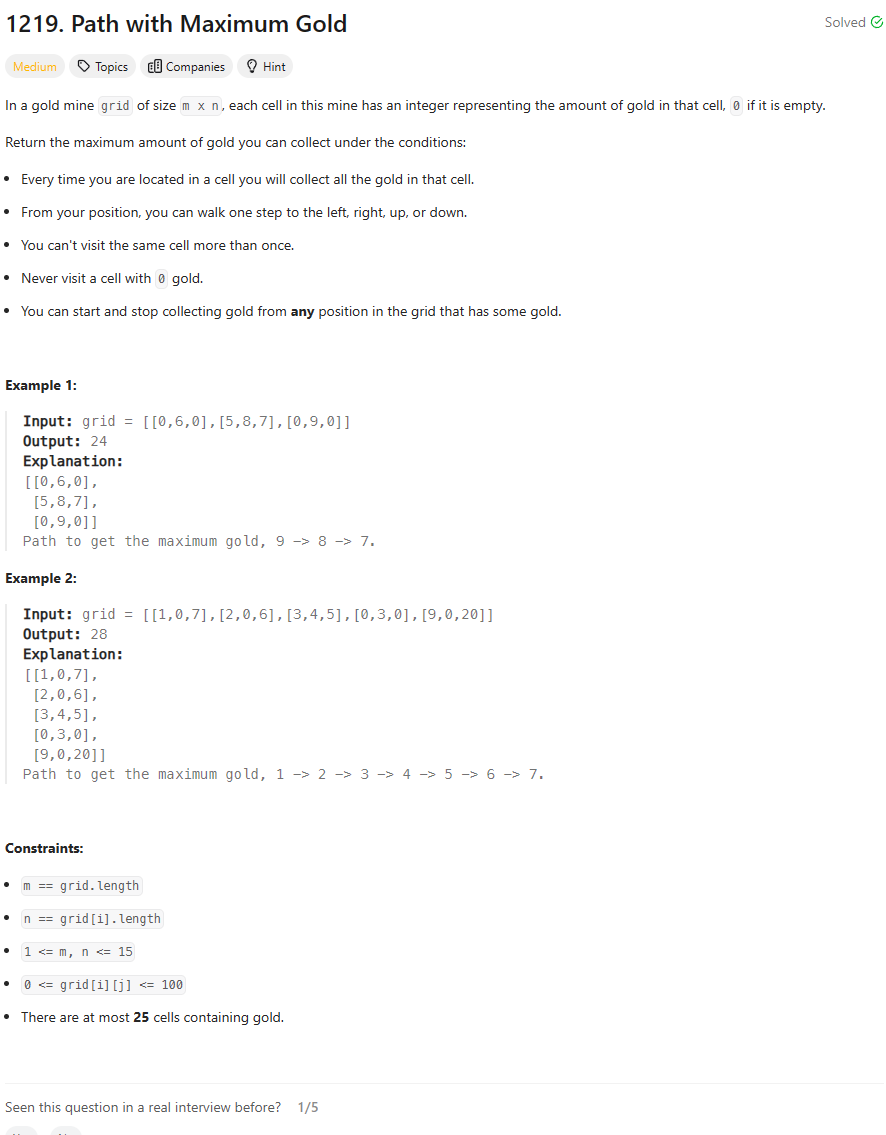
Intuition

When attempting to solve the problem of finding the maximum amount of gold that can be collected in the grid, my first thought is to explore each possible starting point and track the path to maximize the gold collected. This suggests a depth-first search (DFS) approach combined with backtracking to explore all potential paths efficiently and revert changes as necessary.

Approach

• Initialization: Determine the number of rows and columns in the grid and initialize the result variable to store the maximum gold collected.
• Depth-First Search with Backtracking:
  • For each cell in the grid, if it contains gold (i.e., value > 0), start a DFS from that cell.
  • During DFS:
    • Mark the current cell as visited by setting its value to 0.
    • Explore all four possible directions (right, down, left, up).
    • For each valid direction (i.e., within bounds and containing gold), recursively continue the DFS.
    • Track the maximum gold collected during the exploration.
    • After exploring all directions, backtrack by resetting the cell value to its original gold amount.
• Update Result: After exploring all cells, update the result with the maximum gold collected from any path.

Complexity

• Time complexity: O(mn * 4^k)

• Space complexity: O(mn)

Code

class Solution:
    def getMaximumGold(self, grid: List[List[int]]) -> int:
        rows = len(grid)
        cols = len(grid[0])
        res = 0

        def backtrack(r, c, curr):
            ans = curr
            temp = grid[r][c]
            grid[r][c] = 0
            for x, y in [(0,1),(1,0),(-1,0),(0,-1)]:
                nr, nc = r + x, c + y
                if 0 <= nr < rows and 0 <= nc < cols and grid[nr][nc] > 0:
                    ans = max(ans, backtrack(nr, nc, curr + grid[nr][nc]))
            grid[r][c] = temp
            return ans


        for row in range(rows):
            for col in range(cols):
                if grid[row][col] > 0:
                    res = max(res, backtrack(row, col, grid[row][col]))

        return res

Editorial Solution

Approach 1: Depth-First Search with Backtracking

class Solution:
    def getMaximumGold(self, grid: List[List[int]]) -> int:
        DIRECTIONS = [0, 1, 0, -1, 0]
        rows = len(grid)
        cols = len(grid[0])
        max_gold = 0

        def dfs_backtrack(grid, rows, cols, row, col):
            # Base case: this cell is not in the matrix or has no gold
            if row < 0 or col < 0 or row == rows or col == cols or \
                    grid[row][col] == 0:
                return 0
            max_gold = 0

            # Mark the cell as visited and save the value
            original_val = grid[row][col]
            grid[row][col] = 0

            # Backtrack in each of the four directions
            for direction in range(4):
                max_gold = max(max_gold,
                               dfs_backtrack(grid, rows, cols,
                                             DIRECTIONS[direction] + row,
                                             DIRECTIONS[direction + 1] + col))

            # Set the cell back to its original value
            grid[row][col] = original_val
            return max_gold + original_val

        # Search for the path with the maximum gold starting from each cell
        for row in range(rows):
            for col in range(cols):
                max_gold = max(max_gold, dfs_backtrack(grid, rows, cols, row,
                                                       col))
        return max_gold

Approach 2: Breadth-First Search with Backtracking

class Solution:
    def getMaximumGold(self, grid: List[List[int]]) -> int:
        DIRECTIONS = [0, 1, 0, -1, 0]
        rows = len(grid)
        cols = len(grid[0])

        def bfs_backtrack(row: int, col: int) -> int:
            queue = deque()
            visited = set()
            max_gold = 0
            visited.add((row, col))
            queue.append((row, col, grid[row][col], visited))
            while queue:
                curr_row, curr_col, curr_gold, curr_vis = queue.popleft()
                max_gold = max(max_gold, curr_gold)

                # Search for gold in each of the 4 neighbor cells
                for direction in range(4):
                    next_row = curr_row + DIRECTIONS[direction]
                    next_col = curr_col + DIRECTIONS[direction + 1]

                    # If the next cell is in the matrix, has gold,
                    # and has not been visited, add it to the queue
                    if 0 <= next_row < rows and 0 <= next_col < cols and \
                            grid[next_row][next_col] != 0 and \
                            (next_row, next_col) not in curr_vis:
                        curr_vis.add((next_row, next_col))
                        queue.append((next_row, next_col,
                                      curr_gold + grid[next_row][next_col],
                                      curr_vis.copy()))
                        curr_vis.remove((next_row, next_col))
            return max_gold

        # Find the total amount of gold in the grid
        total_gold = sum(sum(row) for row in grid)

        # Search for the path with the maximum gold starting from each cell
        max_gold = 0
        for row in range(rows):
            for col in range(cols):
                if grid[row][col] != 0:
                    max_gold = max(max_gold, bfs_backtrack(row, col))
                    # If we found a path with the total gold, it's the max gold
                    if max_gold == total_gold:
                        return total_gold
        return max_gold